Essence of Chaos: Experiments and Simulations With Marbles and Tubes
Posted:
A guest post by Dr. Abram Hindle, TWOSE Science Fellow, for Science Literacy Week 2020. Abram discusses one of his favourite science books and gives us an experiment, inspired by that book, to try from home!
Hi! My name is Abram Hindle and I’m a TWOSE Science Fellow. One of my favourite science books is Edward Norton Lorenz’s “The Essence of Chaos”. Lorenz was a mathematician and meteorologist who was frustrated by how challenging it is to use computer models to predict the weather. Weather is a dynamic system full of patterns that we can anticipate and name—such as thunderstorms—but some of this behaviour is hard to predict very far into the future. Currently we’re quite good at estimating if it will rain or snow today but our further predictions of rain or snow a week from now are much poorer. Lorenz wanted to understand why some systems act unpredictably under certain conditions and very predictably under other conditions. By predictable, Lorenz means that we can accurately estimate what will happen.
Often chaotic systems exhibit repeated patterns but how and when they do this is often unpredictable. In the cases of turbulent water and the patterns of oil or soap on water, these are examples of chaotic systems whereby we know which patterns are commonly seen but predicting the specific pattern at a given time is very difficult. A big takeaway from Lorenz’s formulation of chaos theory is that systems composed with simple rules can still be unpredictable, depending on initial conditions.
Lorenz’s book, “The Essence of Chaos” is full of examples and simulations of these behaviours. As a software developer and computer scientist myself I am drawn to the simulations, as they demonstrate simplified versions of the complex patterns in nature. As a programmer, it is very satisfying to easily make programs that mimic nature. One chaotic experiment in the book is the simulation of a skier sliding down a bumpy hill full of moguls.
Experiment at home
We can replicate this experiment to demonstrate predictability given initial starting conditions. How can you play around with chaos theory at home? Let’s run an experiment with cardboard tubes and marbles!
In a simplified version of Lorenz’s mogul experiment, we will test how the slope of a ski hill can make the skier’s path hard to predict. In our experiment, we’ll roll marbles (skiers) down a cardboard tube (ski hill). The behaviour that we are studying is the interaction of a marble rolling down a tube. Will we be able to predict where the marble exits the tube consistently? Will different slopes (steepness’s) make it easier or harder to predict the marble’s exit? We’ll find that different steepness are easy to predict while other steepness’s result in more variation in the exit points of the marble.
For this experiment, you’ll need:
- a marble or ball
- a tube, such a paper towel or toilet paper tube, or rolled up paper.
- a ruler or tape measure
- 3 colours of pencil or marker to mark the start and exit positions
- a piece of paper to record data
- 2-10 books
- masking tape
We’re going to drop the marble down the tube and guess where the marble will exit the tube.
- If the tube is very steep, likely we’ll be able to predict that the marble will roll almost in a straight line down the tube or surface and exit in almost the same position each time.
- If the tube is not steep, likely we’ll have a hard time predicting where it will come out because it has a chance to roll side to side.
- If the tube is nearly flat, it probably can’t climb up the sides and will just roll out the middle.
So the game to play is to record the angle that your surface is at, and the distance from the final starting position to the exit position (where it flies out of the tube). Repeat this 5 to 10 times for each steepness (lots, a bit, nearly flat). Reliable experiments in probability typically repeat the trials many times.
Try it yourself! Detailed instructions can be found at the bottom of this post.
Interpreting the Results
Look at the exit positions and answer these questions:
- What steepness of the tube produces the greatest range of positions?
- What steepness of the tube produces the smallest range of positions?
If you can answer the first question you know the conditions for creating a chaotic system.
If you can answer the second question you know the conditions that make for a predictable system.
But in both cases, you are using the same materials and the same system. This is Lorenz’s point. Some initial starting conditions, the starting position and steepness, will produce far more chaotic results than others.
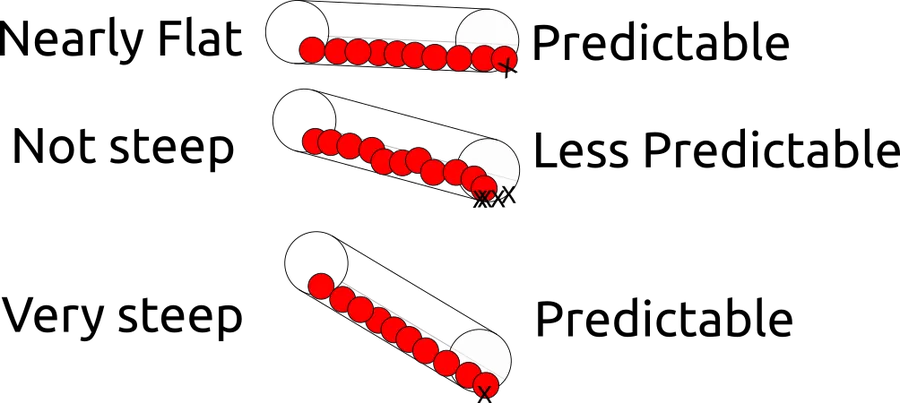
A diagram showing three experimental trials and Abram's results for each trial.
Simulate at home
What drew me to Lorenz’s book is that I like to create programs. I to make programs that simulate experiments in real time on the computer. Personally I am also very lazy and I would prefer if the computer could do the repetitive and hard work for me, such as the in experiment I laid out above.
I coded up a simulation of this experiment, it can simulate 100s of marbles rolling down a half tube (half pipe) all on a web page. The tube is 1 meter long and has a diameter of 5cm. Multiple marbles will roll down the tube leaving a yellow trace of their path. The marbles are placed within 5mm of each other to simulate inconsistency present in physical experiments.
You have control over the steepness of the tube and where the marble starts on the top edge of the tube.
- What steepness of the tube yields the greatest range of positions?
- What steepness of the tube yields the smallest range of positions?
Now this is a simulation so it is simplified version of physics, but you should be able find similarity between your experiment and the simulation, but also find some surprising differences.
[If the simulation below doesn't work from your device, you can also access it from Abram's website: https://softwareprocess.es/2020/pipe/pipe.html]
Comparing the Simulation and the Experiment
Some interesting observations I made from the simulation:
- The marbles roll down the tube in wave-like fashion the further they start from center, so given the right settings you can find parameters where the exit points of the tube converge to a focused range or diverge in a wide range.
- 99% grade is very steep, the marbles flow down the tube very quickly so they don’t interact with the tube for very long, this helps reduce the exit range.
- The 1% grade (very flat) means that it takes a long time for the marble to roll down the tube. What this does is compound the small differences in marble positions and the forces, such as the slope of the tube versus gravity, upon the marbles and sometimes make the range somewhat wider than the 99% case. This build up of little differences can produce unpredictable results.
Book information
https://uwapress.uw.edu/book/9780295975146/the-essence-of-chaos/
Title: The Essence of Chaos
By Edward N. Lorenz
PUBLISHED: October 1995
SUBJECT LISTING: Science and Technology Studies
BIBLIOGRAPHIC INFORMATION: 240 Pages
ISBN: 9780295975146
Try the experiment yourself!
You’ll need:
- a ball or marble
- a tube, such a paper towel or toilet paper tube, or rolled up paper
- a ruler or tape measure
- 3 colours of pencils or markers to mark the start & exit positions
- a piece of paper to record your data
- 2-10 books
- masking tape
Experimental Condition 1: Nearly Flat
- Draw a mark on one end of your cardboard tube (both inside and out) – this will be your starting location.
- Place your cardboard tube flat with the starting point on the bottom. Tape the tube down so that it doesn’t roll around.
- Choose one colour of pencil and keep it nearby. You’ll use this colour to mark the marble’s exit point for this round of the experiment.
- Roll your marble through the cardboard tube: starting with the marble carefully placed at our starting location. Make sure to watch where it exits!
- Using the coloured pencil, which you chose earlier, mark the location where the marble exited the tube.
- Repeat! Keep rolling the marble through the tube – starting at your marked starting location – and marking it’s exit point.
Are the exit points that you marked close together? This indicates that the marble’s behaviour is very predictable under this set of conditions.
Experimental Condition 2: Not Steep
- Create a pile with only 1 book on the table. If you’re able, make sure that a hardcover book is on top (the tape is less likely to damage it).
- Place your cardboard tube so that the starting position is on top of the books and the end of the tube is on the table. It should be positioned to create a slight angle. (If your tube is sitting at a steep angle, remove some books).
- Gently tape the tube down so that it doesn’t roll. Make sure the starting point is on the bottom.
- Choose another colour of pencil for this round of the experiment.
- Roll your marble through the cardboard tube: starting with the marble carefully placed at our starting location. Make sure to watch where it exits!
- Using the coloured pencil you chose earlier, mark the location where the marble exited the tube. These marks should be a different colour than in experiment 1.
- Repeat! Keep rolling the marble through the tube – starting at your marked starting location – and marking it’s exit point.
Are the exit points the same as in experiment 1? If not, are they closer together or further apart? If they are further apart, it means that the marble’s behaviour is less predictable when rolling down a shallow slope.
Experimental Condition 3: Steep Slope
You know the drill! Let’s set up our third experiment.
- This time create a tall pile of books on the table. It should be able ¾ of the height of the cardboard tube.
- Place your cardboard tube so that the starting position is on top of the books and the end of the tube is on the table. It should be positioned to create a steep angle. (If your tube is vertical you have too many books and should remove some).
- Gently tape the tube down so that it doesn’t roll. Make sure the starting point is on the bottom.
- Choose the last coloured pencil for this round.
- Roll your marble through the cardboard tube: starting with the marble carefully placed at our starting location. Make sure to watch where it exits!
- Using the coloured pencil you chose earlier, mark the location where the marble exited the tube. These marks should be a different colour than in experiments 1 & 2.
- Repeat! Keep rolling the marble through the tube – starting at your marked starting location – and marking it’s exit point.
Now you can compare the exit points for all 3 experimental conditions!
Related Articles


Why I Became A Psychologist Who Studies Animals
A guest post by Dr. Lauren Guillette, TWOSE Science Fellow, for Science Literacy Week 2020. Lauren discusses why she became a psychologist who studies animals and her favourite science books.


Be Very, Very Quiet...
This week we are celebrating Science Literacy Week all across Canada! The theme this year is biodiversity, an excellent opportunity for Nature Exchange to explore a new part of nature. To celebrate, I examined some of the biodiversity within The TELUS World of Science Centre - Edmonton's backyard (otherwise known as Coronation Park). Some organisms were easy to find but others were much, much harder.
One of the most plentiful, and hardest to find, is the microscopic master of disguise, the tardigrade.


#TWOSEreads
A collection of book recommendations from our staff in celebration of Science Literacy Week 2020.
Related Articles


Why I Became A Psychologist Who Studies Animals
A guest post by Dr. Lauren Guillette, TWOSE Science Fellow, for Science Literacy Week 2020. Lauren discusses why she became a psychologist who studies animals and her favourite science books.


Be Very, Very Quiet...
This week we are celebrating Science Literacy Week all across Canada! The theme this year is biodiversity, an excellent opportunity for Nature Exchange to explore a new part of nature. To celebrate, I examined some of the biodiversity within The TELUS World of Science Centre - Edmonton's backyard (otherwise known as Coronation Park). Some organisms were easy to find but others were much, much harder.
One of the most plentiful, and hardest to find, is the microscopic master of disguise, the tardigrade.


#TWOSEreads
A collection of book recommendations from our staff in celebration of Science Literacy Week 2020.





